Solved: Math 104, Section 101 : Extra Exercises #3
Instructions : Show all your work. Remember to be as clear as possible and to give reasons for your answers. 1. An ice cube melts at a rate proportional to its surface area. The length of the side of the cube is 2 cm at 1:00 pm and 1.5 cm at 2:00 pm. When will the cube be completely melted? 2. An isosceles triangle (two sides have equal length) has a perimeter equal to 3 cm. What is the maximum area the triangle can have? 3. The function f has a derivative defined and continuous for all x. f has critical points at x = 0, 1 and 2, and f(−1) = 1, f(0) = 0, f(1) = 1, f(2) = 2 and f(3) = 1. List all points for which f has a local maximum. 4. Suppose that g is a differentiable function with the property that g(0) = 2 and with the tangent line to the graph of y = g(x) at (0, 2) given by y = 6x + 2. If we also know that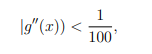
for all values of x, find a value of M (as small as possible) such that the error in using the tangent line as an approximation to g(x) in the interval [−3, 3] is at most M.
5. Find the interval or intervals where h(x) = x1/3(x2 − x − 3) is increasing.