Solved: EXPLORATION 10.4: Perceptions of Heaviness 247
Researchers believe a person’s body is used as a perceptual ruler and people will judge the size of an object based on its relationship to parts of their body. Specifically, some researchers thought people with smaller hands will perceive objects to be bigger and hence heavier than those with larger hands. Linkenauger, Mohler, and Proffitt (2011) collected data on 46 participants, recording their hand width and estimated weight of bean bags. The results are shown in Table 10.4.
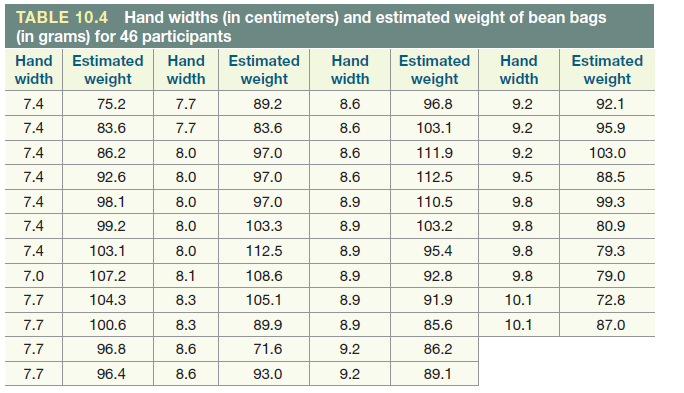
- Write the null and alternative hypotheses for this study in words (use the term “association”).
In Section 10.2 we used the Corr/Regression applet to perform a simulation-based test for a correlation coefficient. Doing the simulation-based test for the slope of the regression line is extremely similar. The only difference is that we use the slope as our statistic instead of the correlation coefficient. The applet has a radio button to select to switch from one statistic to the other. - Paste the data, hand width, in the Corr/Regression applet and make a scatterplot. Describe the direction, form, and strength of the scatterplot.
- Use the applet to determine the least squares regression line for predicting estimated weight based on hand width. What is the value of the slope of the regression line? What does this number imply in terms of hand width and estimated weight?
- You should have found a negative association between hand width and estimated weight of the bean bag in the sample. The question, however, is if there were no association between hand width and the weight of an object in the population, how likely is it that we would get a slope as small (as far below zero) as we did. Let’s apply the 3S strategy.
a. Statistic: What is the value of the slope in the sample?
b. Simulate: To simulate you can use the same general approach we used for correlation in Section 10.2. Explain how you would conduct the approach by hand. Assume you have 46 slips of paper with the sample hand widths written on them and 46 slips of paper with the perceived weight values written on them.
c. Strength of evidence: Explain how you will calculate the strength of evidence in support of the conjecture that people with larger hands tend to perceive less weight in the bean bags. - Now let’s complete a test of significance.
a. Let’s shuffle the response variable (estimated weight) and see what we get for sample slope values when we break the association between the data pairs. Use the applet to do this five times and write down the five simulated slopes you get. Are any of them as small as or smaller than the value of the actual sample slope?
b. Now do at least 1,000 shuffles with the applet and find the p-value.
c. Click on Plot in the Shuffle Options section of the applet. Th is will now display each of the 1,000 simulated regression lines (in blue). Describe the behavior of the 1,000 regression lines across the different shuffles (see FAQ 10.4.1 for some discussion about this).
d. Explain what your p-value measures in the context of the study.
e. Can we conclude that there is strong evidence of a genuine negative association between hand width and estimated weight of the object in the population?
What is the point of averages? - As you did in Section 10.2, find the p-value corresponding to the correlation coefficient.
How does this p-value compare with the p-value corresponding to the slope? (Note: You should have the p-value for the slope in #5(d).)
For a given data set, the test for slope is equivalent to the test for correlation coefficient.
K E Y I D E A
For a given data set, the test for slope is equivalent to the test for correlation
coefficient.
- The sample used here was not a random sample. The article just said that the researchers obtained data on 46 participants.
a. Describe the population to which we could legitimately make our inference. Explain your reasoning.
b. Can we conclude that having smaller hands causes a person to estimate the weight of the bean bag to be larger? Explain your answer.

